| NAVAL ORDNANCE AND GUNNERY, VOLUME 2 CHAPTER 23 AIRCRAFT FIRE CONTROL |
| HOME INDEX Chapter 23 Aircraft fire control A. Introduction B. Aircraft gunnery C. Aircraft weapon systems D. Theory of horizontal bombing E. Other bombing problems F. Rocketry |
| D. Theory of Horizontal Bombing 23D1. General Study of the action of a bomb in air must be started from some situation with which we are familiar. The condition selected for a start, therefore, is the bomb’s action when dropped in a vacuum. The established laws of physics give us formulas for the speed of a falling body, which are expressed in terms of the attraction of gravity and the amount of time or the distance through which it acts. The body will pick up speed or accelerate at a constant rate known as the acceleration of gravity. At sea level this acceleration is about 32.2 feet-per-second per second and is called “g.” The formulas for computing the speed of a falling body in a vacuum are: |
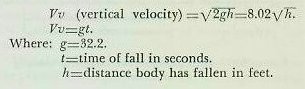 |
| Vacuum trajectory. Due to the fact that a bomb is always dropped from a moving airplane, the bomb in a vacuum would retain, during its time of fall, any horizontal motion imparted to it by the plane, and this motion would remain constant in magnitude and direction. If the aircraft did not alter its course or speed, the bomb would remain vertically below the plane as it fell and the plane would be directly over the point of impact when the bomb hit. The parabolic path that the bomb would follow when dropped from a moving plane is called the vacuum trajectory. |
 |
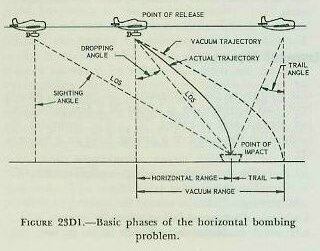 |
| 23D2. Range problem Since, in fact, air does exert a resistance upon the bomb, it has the following important effects: 1. It decreases the vertical velocity at any instant and thereby increases the time of fall. 2. It causes the horizontal velocity to diminish and thus causes the bomb to trail behind the vertical from the plane. The above effects vary with: 1. Shape, weight, and skin friction of the bomb. 2. Altitude. 3. Air speed. Figure 23D1 illustrates the basic phases of the horizontal bombing problem and shows the difference between an actual and a vacuum trajectory. In using figure 23D1 the following definitions apply: 1. Sighting angle. At any instant the angle between the LOS and the true vertical determined by the bomb sight gyro (spin axis). 2. Dropping angle. The angle between the LOS and the spin axis of the bomb sight at the instant of release. At this instant the sighting angle is equal to the dropping angle. 3. Trail angle. The angle between the spin axis of the bomb sight and the LOS at the time of impact, if the airplane maintains course and speed. 4. Horizontal range in air. The horizontal distance that the bomb travels between release and impact. 5. Trail (T). The horizontal distance between the points of impact of an actual trajectory and a vacuum trajectory. 6. Horizontal range in vacuum. Equal to horizontal range in air, plus trail. |
| Trail is primarily caused by the horizontal force (air resistance) acting on the bomb after release. Since the bomb is released in the direction of the plane’s motion, the trail is always astern of the aircraft. The amount of trail is dependent upon two factors: 1. The amount of air resistance, which is equivalent to the indicated air speed of the plane at the time of release. 2. The length of time that air resistance acts on the bomb, which is equivalent to the altitude of release. The actual trail and time of fall values for each type of bomb are determined at the proving ground and appropriate tables are prepared. Trail is always expressed in angular measure (mils) and the amount of trail is called trail angle. |
 |
 |
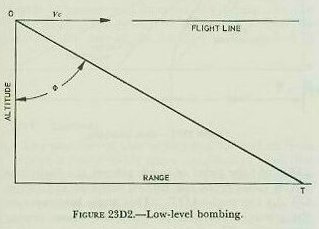
| This equation shows the close dependence of the dropping angle on altitude and closing speed. Hence, unless the altitude and closing speed can be held very closely to pre-assigned values, errors in these quantities will produce large range errors on the ground. See figure 23D2. |
 |
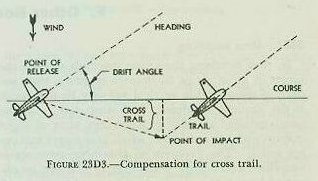 |
| 23D3. Drift problem Discussion to this point has been based on conditions of either still air or wind that is either up or down the plane’s heading. Since bombing only up or down wind is not practical, the bomb sight is designed to bomb on any course regardless of wind. To do this, means are provided whereby the bomber may direct the pilot to steer a course which will cause the plane’s track to pass through the proper position with respect to the target so that the bomb will hit. When an aircraft is headed directly up or down wind, it is making good over the ground the course steered. On any other course, with the wind somewhere to the side, the course made good is not that steered, but a resultant of the plane’s course and speed and that of the wind. The angle thus formed between the heading of the plane in the air and its direction of movement over the earth is known as drift angle. It is obvious that any cross wind will act not only upon the plane but also upon the bomb after release, and compensation must be made. If the bomber were merely to direct the pilot to continuously head the plane for the target, the path over the ground would be constantly changing and eventually the plane would be headed into the wind, the drift angle would be zero, and the plane would pass directly over the target. With such a method the bombing problem is constantly changing and the bomber would never solve the problem correctly. If the effects of a cross wind could be taken into account and the correct drift angle set up, the approach would be direct and constant, and the dropping angle could then be easily solved. Establishment of the correct drift angle involves the setting up of a collision course with the target. The fact that the plane is flying horizontally above sea level does not introduce difficulties, for we can simply consider the plane’s projection on the surface as being put on a collision course. This method does introduce a small lateral error known as cross trail, but it is compensated for in the bomb sight. This compensation causes the plane to be flown on a track to one side of the target by an amount equal to the value of cross trail. Figure 23D3 illustrates the necessity of compensating for cross trail. The same consideration for target motion across the plane’s heading is made as was for target motion along the heading in the range problem. It is considered as a cross wind and is absorbed as such in the bomb sight solution. The solution of the bombing problem is done by the bomb sight in terms of angles rather than distances, and for this reason all values with the exception of altitude are put into the bomb sight as angles in the form of mils; a mil being the angle subtended by an arc whose length is one-thousandth of the range. The above discussion concerned only horizontal bombing, which serves as a basic model for all types of bombing problems. It also concerned the use of the Mark 15 visual bomb sight. During and since World War II radar sights have been extensively employed. They present one great advantage; namely, that an attack is possible without visual sight of the target. An offset aiming feature in the radar sight makes possible the hitting of a poorly defined radar target by using some other well defined object as a reference point. In horizontal bombing a compromise must be reached between low and high altitude of attack. Generally, low altitude provides maximum accuracy but gives minimum protection against interception and antiaircraft fire. High altitude gives better protection but less accuracy, and the target must be large enough to be vulnerable over a considerable area. Horizontal bombing does not place undue stresses on the aircraft structure and therefore the plane is able to carry a comparatively large payload. |